"영축력(盈縮曆)"의 두 판 사이의 차이
(XML 가져오기) |
(차이 없음)
|
2017년 12월 10일 (일) 02:36 기준 최신판
| 주요 정보 | |
|---|---|
| 대표표제 | 영축력 |
| 한글표제 | 영축력 |
| 한자표제 | 盈縮曆 |
| 관련어 | 영축가분(盈縮加分), 영축적(盈縮積), 영축차(盈縮差), 중심차(中心差), 초차법(招差法) |
| 분야 | 문화/과학/천문 |
| 유형 | 개념용어 |
| 지역 | 한국 |
| 시대 | 조선 |
| 집필자 | 이은희 |
| 조선왕조실록사전 연계 | |
| 영축력(盈縮曆) | |
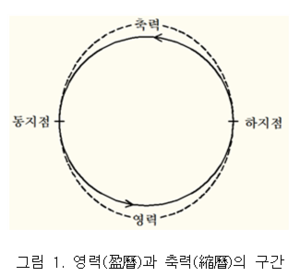
진태양(眞太陽)이 평균태양보다 앞서는 구간인 영력(盈曆)과, 평균태양이 진태양을 앞서는 구간인 축력(縮曆)을 합쳐서 이르는 말.
개설 및 내용
고대 중국에서는 태양이 하루에 1도씩 움직인다고 여겼기 때문에, 태양이 하늘을 한 바퀴 도는 데 걸리는 1년의 일수(日數)가 하늘의 둘레인 주천(周天)의 도수(度數)와 같다고 생각하였다. 즉 원둘레의 도수를 1년의 일수와 같게 생각하였는데, 당시 중국의 1도(度)는 서양의 방법을 따르는 오늘날의 도법(度法)으로는 0.9856°에 해당한다. 원나라 때의 역법인 『수시력(授時曆)』에서는 1년의 길이를 365.2425일로 정하였으므로, 이때 태양이 하늘을 한 바퀴 도는 도수는 365.2425도가 된다. 그러나 관측 기술이 발달하면서 태양이 하루에 1도씩 등속도로 움직이는 것이 아니라, 태양의 운동이 빨라지거나 느려지는 현상 즉 일행영축(日行盈縮)의 현상이 일어난다는 사실을 발견하게 되었고, 이를 진태양의 위치를 구하는 데 사용하게 되었다. 이러한 현상은 지구가 태양 주위를 원궤도가 아닌 타원궤도로 운동하기 때문에 생기는 것으로, 케플러의 법칙에 따라 지구는 근일점(近日點)에서 가장 빠르게 움직이고 원일점(遠日點)에서 가장 느리게 움직인다.
이와 같이 태양의 운행이 빨라지거나 느려지는 현상은 겉보기운동에서 부등운동을 하는 진태양과 1일 1도의 등속운동을 하는 평균태양의 거리인 중심차(中心差)란 이 가상의 태양과 부등운동을 하는 진태양과의 상거도(相距度) 즉, 떨어진 각거리(角距離)를 의미한다. 『수시력』의 역원(曆元)인 1281년 당시, 우연히도 근일점은 동지점(冬至點)과, 원일점은 하지점(夏至點)과 거의 일치하였다. 따라서 태양의 운동 속도는 동지와 하지를 전후로 각각 대칭이 되었다. 즉 추분에서 동지와 동지에서 춘분 사이가 대칭이 되었고, 또 춘분에서 하지와 하지에서 추분 사이가 대칭이 되었다. 그런데 태양의 실제 속도가 평균 속도인 1도보다 빠른 동지 전후의 상한(象限) 즉, 추분에서 동지까지와 동지에서 춘분까지는 태양이 각 상한 91.31도를 88.91일 만에 운행하는 반면, 평균 속도인 1도보다 느린 하지 전후의 상한 즉, 춘분에서 하지까지와 하지에서 추분까지는 각 상한 91.31도를 93.71일이 되어서야 운행을 마치게 된다. 여기서 진태양이 1도 이상 움직이는 행도(行度)를 영행도(盈行度), 영행도와 평균태양의 행도 차를 영가분(盈加分), 그리고 영가분의 누적분을 영적(盈積)이라고 한다. 마찬가지로 진태양이 1도 이하로 운행하는 행도를 축행도(縮行度), 축행도와 평균 행도와의 차를 축가분(縮加分), 축가분의 누적분을 축적(縮積)이라고 한다. 결국 동지에서 하지까지는 진태양이 평균태양보다 앞서는 영력 구간이 되고, 하지에서 동지까지는 진태양이 평균태양에 뒤지는 축력 구간이 된다.
동지와 하지를 전후한 2상한(象限)의 영축(盈縮)과 행도의 값은 『수시력』과 『대통력(大統曆)』, 그리고 『칠정산내편(七政算內篇)』의 입성(立成)에 각각 기록되어 있다. 진태양의 위치는, 구하고자 하는 날이 동지와 하지를 전후로 몇 번째 날인지를 입성에서 확인하여 영력과 축력을 정하고, 다시 각각의 구간에서 영가분과 축가분을 구한 뒤, 평균태양이 위치한 곳에서 더하거나 빼서 계산한다. 여기서 더하고 뺄 때 사용하는 영축차(盈縮差)는 중심차를 가리키는데, 진태양이 위치하는 곳과 평균태양이 위치하는 곳 사이의 각거리 즉 각도 차를 의미한다. 『수시력』에서는 이 중심차를 계산하기 위하여 1원 3차 방정식인 초차법(招差法)을 창안하였다. 초차법은 평립정삼차(平立定三差)의 보간식을 이용하여 평차(平差), 입차(立差), 정차(定差)의 계수를 구하는 방법으로, 이들은 실측한 태양의 영축 값들로부터 구한다. 『대통력』의 법원(法原)에 실려 있는 ‘태양영축평립정삼차지원(太陽盈縮平立定三差之原)’의 입성에서는 1년 사상한(四象限) 중 영초축말한(盈初縮末限) 88.92일의 경우 각 단(段)을 14.82일씩 6단으로 등분하였고, 축초영말한(縮初盈末限) 93.72일의 경우 각 단을 15.62일씩 6단으로 등분하여 각 상한의 정차와 평차 그리고 입차를 구하였다. 이들 계수는 임의의 적일(積日)의 영축적 값을 구하는 데 사용되었다. 이때 적일을 1일 간격으로 하지 않고 각 상한을 6단으로 등분하여 2주 간격으로 계산한 것은 1일 사이의 평차와 그 차의 차가 너무 작아지면 오차가 커질 것을 우려하였기 때문이다. 이와 같은 초차법은 일행영축뿐 아니라 오행영축(五行盈縮)의 중심차 계산에도 사용되었다. 일행영축의 중심차인 영축차의 계산은 다음의 식을 따른다.
영축차 = 영축적(盈縮積) + 입한분(入限分) ⨉ 영축가분(盈縮加分)/10,000
= x(t) + Δ(t)‧δx/10,000
(t: 입한일, x(t): t일의 영축적, Δ(t): 입한분, δx: 영축가분일 때)
변천
태양이 부등운동을 한다는 사실을 중국에서 가장 먼저 발견한 사람은 6세기 중엽 북제(北齊)의 천문학자인 장자신(張子信)이었다. 서양에서는 기원전 2세기경에 그리스의 히파르코스(Hipparchos)가 발견하였으므로, 중국에서의 발견은 서양에 비해 700년가량 늦은 셈이 된다. 수(隋)나라 때의 장주현(張胄玄)은 『대업력(大業曆)』에 태양의 부등운동을 도입하였다. 비슷한 시기에 유작(劉焯)은, 태양의 부등운동으로 인해 각 평기(平氣) 사이에서 태양이 움직이는 도수가 일정하지 않으므로 태양의 실제 위치로 절기를 나누는 정기법(定氣法)을 사용할 것을 제안하면서 자신이 만든 『황극력(皇極曆)』에 이를 적용하였다. 그러나 중국에서는 『황극력』 이후로도 계속해서 일정한 도수로 나누는 평기법(平氣法)을 사용하였으며, 명나라 때 서양 역법을 바탕으로 만들어진 『시헌력(時憲曆)』에 이르러서야 비로소 태양의 부등운동에 따른 정기법을 채택하였다.
태양의 부등운동은 『황극력』과 그 뒤 당(唐)나라 때 일행(一行)이 만든 『대연력(大衍曆)』에서 특별한 형태로 나타났다. 즉, 이들 역법에서는 정기(定氣)에 따른 각 절기 사이의 길이가 태양의 빨라지고 늦어짐에 따라 변한다는 사실에 착안하여 각 절기의 길이를 일수(日數)로 표시하였다. 『대연력』이 쓰였던 727년경에는 태양이 가장 빠르게 움직이는 것은 동지 9일 전쯤이었는데, 이것을 거의 동지라고 생각하였다. 이와 같은 생각은 원나라 때의『수시력』으로 이어졌고,『수시력』을 편찬할 당시의 근일점은 실제로 거의 동지와 일치하였다. 그에 따라 정기 사이의 일수는 태양이 근지점(近地點)을 통과할 때 가장 짧고, 그 전후의 일수는 거의 대칭을 이루었다.
한편 중국에서는 태양의 부등운동 즉, 일행영축을 계산할 때 태양이 근지점을 통과할 때를 기준으로 하였으나, 프톨레마이오스(Ptolemaeos)의 『알마게스트(Almagest)』로 대표되는 그리스 역법에서는 원지점(遠地點)을 기준으로 삼았다는 차이점이 있다. 또 중국에서는 해와 달의 부등운동으로 인해 생기는 중심차 문제를 계산하기 위하여 여러 가지 노력을 하였다. 수나라의 유작은 가우스(Gauss) 보간법에 해당하는 2차 보간법을 발명하였으며, 당나라 말기의 변강(邊岡)은 호수림(胡秀林), 왕지(王墀) 등과 함께 제작한 『숭현력(崇玄曆)』에서 상감상승법(相減相乘法)을 사용하였다. 그 뒤 『수시력』에 이르러서는 좀 더 정밀한 3차 보간법인 초차법이 창안되어 해와 달의 운동을 정확하게 표현할 수 있게 되었다.
참고문헌
- 藪內淸 著, 兪景老 譯, 『中國의 天文學』, 전파과학사, 1985.
- 유경로·이은성·현정준 역주, 『세종장헌대왕실록』 「칠정산내편」, 세종대왕기념사업회, 1973.
- 이은성, 「招差法과 古代曆法에서의 그 應用」, 『천문학회지』7-1, 1974.
- 이은희, 『칠정산내편의 연구』, 한국학술정보, 2007.
- 藪內淸, 『隨唐曆法史の硏究』, 臨川書店, 1989.
관계망