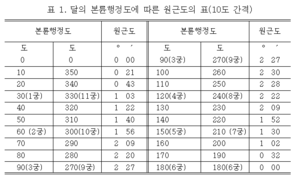
"원근도(遠近度)"의 두 판 사이의 차이
(XML 가져오기) |
(차이 없음)
|
2017년 12월 10일 (일) 02:34 기준 최신판
| 주요 정보 | |
|---|---|
| 대표표제 | 원근도 |
| 한글표제 | 원근도 |
| 한자표제 | 遠近度 |
| 상위어 | 본륜(本輪), 소륜(小輪), 주전원(周轉圓) |
| 관련어 | 근지점(近地點), 본륜행정도(本輪行定度), 소륜심정도(小輪心定度), 원지점(遠地點) |
| 분야 | 문화/과학/천문 |
| 유형 | 개념용어 |
| 지역 | 한국 |
| 시대 | 조선 |
| 집필자 | 안영숙 |
| 조선왕조실록사전 연계 | |
| 원근도(遠近度) | |
달이나 행성의 주전원(周全圓)의 중심이 근지점(近地點)에 있을 때 천체와 근지점의 이각(離角)과, 주전원의 중심이 원지점(遠地點)에 있을 때 지구에서 본 천체와 원지점의 이각의 차(差).
개설
고대 그리스에서는 우주의 중심이 지구이고, 태양과 달 등의 천체는 원운동을 하는 지구를 이심(離心)으로 하는 이심원을 따라 공전한다고 생각하였다. 그리고 지구 주위를 도는 천체들은 이 이심원의 원주에서 다시 작은 원을 그리며 돌고 있다고 여겼다. 이때 이 작은 원을 주전원(周全圓)이라고 한다. 이 학설은 지구중심설 또는 천동설이라고 하는데, 고대 그리스의 프톨레마이오스(Ptolemaios)에 의해 도입되었다. 『칠정산외편(七政算外篇)』에서는 달의 주전원을 본륜(本輪)이라 하고, 행성의 경우는 소륜(小輪)이라고 표현하였다.
내용 및 특징
원근도(遠近度)는 천체의 주전원의 중심이 지구의 원지점이나 근지점에 위치할 때, 주전원 위의 천체와 주전원의 중심이 이루는 각을 지구에서 바라보았을 때의 값의 차이이다. 『칠정산외편』에서는 이 개념을 달과 행성의 운동에 적용하였다.
1) 달의 원근도
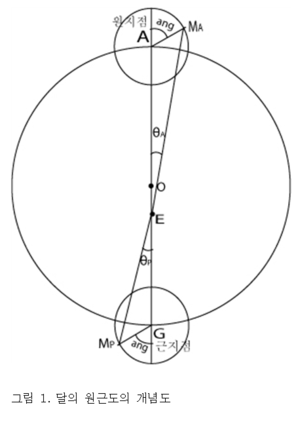
지구가 원궤도의 중심에 있지 않고 이심점에 있으므로, 달은 궤도운동을 하면서 본륜의 중심이 원지점에 있을 때와 근지점에 있을 때가 있다. 이때 이심점인 지구에서 원지점이나 근지점에 있는 본륜의 중심과 본륜 위의 달이 이루는 각도는 각각 다르게 되는데, 이 두 값의 차이가 원근도이다. 이때 본륜행정도(本輪行定度)는 같다고 본다. 그림 1을 참고하여 설명하면 다음과 같다.
달의 주전원인 본륜의 중심이 근지점 G에 있을 때 달 MP와 G의 이각(離角)인 θP에서, 본륜의 중심이 원지점 A에 있을 때 달 MA와 A의 이각인 θA를 뺀 값이 바로 원근도이다. 원지점과 근지점의 각 위치에서 달의 본륜행정도가 같으면, 원지점에서의 ∠AEMA보다 근지점에서의 ∠GEMP가 더 크다. 결국 원근도는 ∠GEMP에서 ∠AEMA를 뺀 값에 해당한다. 그림 1은 다음 식으로 나타낼 수 있다.
원근도 = ∠GEMP - ∠AEMA = θP - θA
이 값은 『칠정산외편』의 ‘달의 경도 제2가감차와 원근도의 표’에 본륜행정도를 인수로 하여 수록되어 있다.
2) 행성의 원근도
행성의 경우도 달과 마찬가지인데, 주전원이 소륜이므로 본륜의 중심 대신 소륜의 중심을 이용한다. 지구 E에서 바라볼 때 원지점 A에서의 소륜의 중심과 소륜 위의 행성 P가 이루는 각을 θA, 근지점 G에서의 소륜의 중심과 소륜 위의 행성이 이루는 각을 θP라고 하면 다음과 같이 나타낼 수 있다.
원근도 = ∠GEPP - ∠AEPA = θP - θA
『칠정산외편』의 ‘5성 경도 제2가감차분과 원근도의 표’에는, 각 행성의 자행정도(自行定度)에 따른 궁도별 원근도 값이 수록되어 있다.
참고문헌
- 『칠정산외편(七政算外篇)』
- 『칠정산외편정묘년교식가령(七政算外篇丁卯年交食假令)』
- 안영숙, 『칠정산외편의 일식과 월식 계산방법 고찰』, 한국학술정보, 2007.
- 유경로·이은성·현정준 역주, 『세종장헌대왕실록』 「칠정산외편」, 세종대왕기념사업회(서울), 1990.
- Toomer, G. J., 『Ptolemy’s Almagest』, Princeton Univ. press(New jersey), 1998.
관계망