"본륜행도(本輪行度)"의 두 판 사이의 차이
(XML 가져오기) |
(차이 없음)
|
2017년 12월 10일 (일) 02:31 기준 최신판
| 주요 정보 | |
|---|---|
| 대표표제 | 본륜행도 |
| 한글표제 | 본륜행도 |
| 한자표제 | 本輪行度 |
| 상위어 | 본륜(本輪), 천동설(天動說) |
| 관련어 | 본륜행정궁도(本輪行定宮度), 본륜행정도(本輪行定度), 제일가감차(第一加減差) |
| 분야 | 문화/과학/천문 |
| 유형 | 개념용어 |
| 지역 | 한국 |
| 시대 | 조선 |
| 집필자 | 안영숙 |
| 조선왕조실록사전 연계 | |
| 본륜행도(本輪行度) | |
주전원인 본륜(本輪)의 원주(圓周) 위에 있는 달의 위치를 기준선으로부터 표시한 각도.
개설
고대 그리스에서는 우주의 중심이 지구이고, 태양과 달 등의 천체는 원운동을 하는 지구를 이심(離心)으로 하는 이심원을 따라 공전한다고 생각하였다. 그리고 지구 주위를 도는 천체들은 이 이심원의 원주에서 다시 작은 원을 그리며 돌고 있다고 여겼는데, 이때 이 작은 원을 주전원(周全圓)이라고 한다. 고대 그리스의 천문학자 프톨레마이오스(Ptolemaeus)에 의해 제기된 이 학설은 지구중심설 또는 천동설이라고 한다. 조선시대 전기의 천문서인 『칠정산외편(七政算外篇)』에서는 달의 주전원을 본륜(本輪)이라 하고, 행성의 경우는 소륜(小輪)이라고 표현하였다.
내용 및 특징
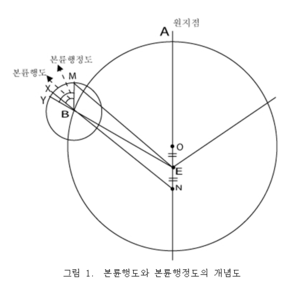
본륜행도는, 달이 본륜의 원주의 한 점인 M에 있을 때, 그 위치를 한 기준선으로부터의 각도로 표시한 것이다. 그림 1에서 보는 바와 같이, 원의 중심 O에서 이심(離心) E까지의 거리 OE를 2배로 연장하여 OE=EN인 점 N을 정한다. N에서 달의 궤도인 본륜의 중심 B까지를 연결한 직선이 B를 지나 본륜의 원주와 만나는 점을 X라고 한다. 이때 선분 NX가 본륜행도를 재는 기준선이다. 보통 점 X는 그 본륜의 평균 원지점의 위치에 해당한다. 그리고 선분 BX와, 본륜의 중심 B에서 본륜 위의 달의 위치인 M까지를 연결한 선분 BM이 이루는 각도가 바로 본륜행도이다. 본륜행도에 제1가감차를 가감하면 본륜행정도(本輪行定度)가 된다.
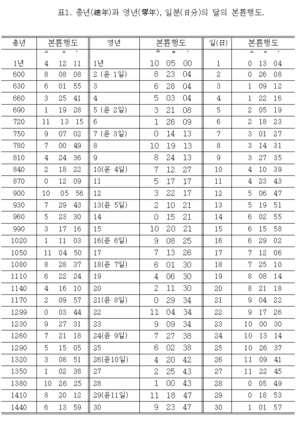
본륜행도의 값은 『칠정산외편』의 ‘달의 중심행도와 가배상리도, 본륜행도의 표’에 정리되어 있다. 그런데 이 표에 수록된 값은 헤지라 기원인 622년 1월 1일을 기준으로 한 것이므로, 『칠정산외편』의 태음력 기점인 598년 4월 13일의 값이 되도록 보정해주어야 한다. 이때 보정 값은 151°00′, 즉 5Δ01°00′이므로, 표에서 구한 값에 이 값을 보정하여 사용한다.
<본륜행도의 표>
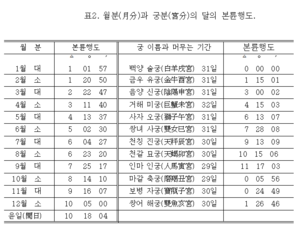
본륜행도의 값은 『칠정산외편(七政算外篇)』의 ‘달의 중심행도와 가배상리도, 본륜행도의 표’에 각 시간 간격별로 수록되어 있다. 표에 제시된 시간 간격은 총년(總年)·영년(零年)·월분(月分)·일분(日分)·궁분(宮分) 등 다섯 종류이다. 각 시간 단위별 본륜행도 값을 살펴보면 다음과 같다.
이 표들은 고대 그리스의 천문학자 프톨레마이오스(Ptolemaeos)가 저술한 『알마게스트(Almagest)』에 ‘달의 평균 운동표(Table of the Moon’s Mean Motion)‘에 이각의 증가분(Increment in Anomaly)으로 수록되어 있다. 그러나 『칠정산외편』과는 시간 간격이 달라 일분 본륜행도 외에는 비교하기가 어렵다. 『칠정산외편』에는 본륜행도 값이 도(度)와 분(分) 단위까지 표시되어 있는 데 비해, 『알마게스트』에는 도 이하 일곱 번째 단위까지 상세한 값이 수록되어 있다. 또한 『칠정산외편』에는 월분은 음력월을 기준으로 29일과 30일 간격으로, 영년은 30년까지, 총년은 30년 간격으로 각각 본륜행도 값이 수록되어 있다. 그에 비해 『알마게스트』에는 월분은 30일 간격으로, 영년은 18년까지, 총년은 18년 간격으로 18년에서 810년까지 각각의 값이 실려 있다.
<본륜행도의 변화량>
본륜행도는 대략 근점월(近點月)을 주기로 원래 위치로 돌아온다. 따라서 본륜행도의 1일 운동량은 원을 근점월인 27.55455일로 나누어서 구한다. 달의 1일 본륜행도 평균 이동량은 13°03′54″(=13°.06499)가 된다. 표에서는 계산의 편리함을 위하여 13°04′씩 더해주고, 중간에 보정을 해준다.
(360도/27.55455) = 13°.06499 = (13°03′53″.96)
<본륜행정도>
본륜행정도(本輪行定度)는 본륜행도에 제1가감차를 더해주거나 빼주는 것으로 정의한다.
<본륜행정궁도>
본륜행정궁도는 본륜행정도를 궁(1궁=30도) 단위와 함께 표현할 때 사용한다. 예를들어, 55°는 1Δ25°(1궁 25도)가 된다. 『칠정산외편』에는 이 값을 인수로 하여 ‘달의 경도 제2가감차분과 원근도의 표’가 수록되어 있다.
참고문헌
- 『칠정산외편(七政算外篇)』
- 안영숙, 『칠정산외편의 일식과 월식 계산방법 고찰』, 한국학술정보, 2007.
- 유경로·이은성·현정준 역주, 『세종장헌대왕실록』「칠정산외편」, 세종대왕기념사업회, 1990.
- Toomer, G. J.,『Ptolemy’s Almagest』, Princeton Univ. press(New jersey), 1998.
관계망